Question

The height of a trapezoid is 6 in. and it’s area is 72 in to the 2nd power. One base of the trapezoid is 6 inches longer than the other base. What are the lengths of the bases? Complete the explanation of how you found your answer.

One base is __ inches for one of the bases and __ inches for the other base.


Use the formula for the area of a trapezoid. Substitute 72 for A and 6 for h and simplify the equation to find __ = (b1 + b2). Use guess and check to find two numbers that add to __ with one number 6 more than the other to get __ inches for one of the bases and __ inches for the other base.

Answer 1

Given:

The height of the given trapezoid = 6 in

The area of the trapezoid = 72 in²

Also given, one base of the trapezoid is 6 inches longer than the other base

To find the lengths of the bases.

Formula

The area of the trapezoid is

`A=(1)/(2) (b_(1) +b_(2) )h`

where, h be the height of the trapezoid

`b_(1)` be the shorter base

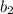`b_(2)` be the longer base

As per the given problem,

`b_(2)=b_(1) +6`

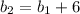
Now,

Putting, A=72,
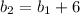`b_(2)=b_(1)+6` and h=6 we get,

`(1)/(2) (b_(1) +b_(1)+6)(6) = 72`

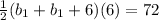
or,
`b_(1)+b_(1)+6 = ((72)(2))/(6)`

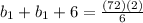
or,
`2b_(1)+6 = 24`

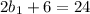
or,
`2b_(1)=24-6`

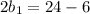
or,
`b_(1)= (18)/(2)`

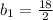
or,
`b_(1)=9`

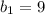
So,

The shorter base is 9 in and the other base is = (6+9) = 15 in

Hence,

One base is 9 inches for one of the bases and 15 inches for the other base.