Question

Find the value of x that makes m ∥ n.

Answer 1

90

Explanation:

Answer 2

Given:

The measures of the alternate exterior angles are (180 - x)° and x°

We need to determine the value x that makes m ║ n

Value of x:

We know that the measures of alternate exterior angles are equal.

Thus, we have;

`180-x=x`

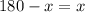
Adding both sides of the equation by x, we have;

`180-x+x=x+x`

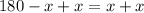
Simplifying, we get;

`180=2x`

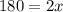
Dividing both sides of the equation by 2, we have;

`90=x`

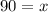
Thus, the value of x is 90.

Hence, the value x = 90 makes the alternate exterior angles congruent and hence the line m is parallel to n.