Answer:
18.85 years
Explanation:
Using the
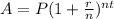 we can manipulate it to give us time.
we can manipulate it to give us time.
However, let's identify our variables:
A is our final amount which is given to us, $1400.
P is our principle which is $500.
r is our rate which is 5.5% which can be traducted into 0.055.
n is the # of time our money get compounded per year, in this case quarterly means 4 times a year therefore n = 4.
t is time and is what we are trying to solve for.
Now let's manipulate our equation to find t:
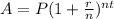
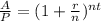
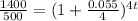

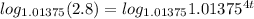

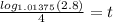
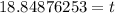
It would take about 18.85 years in order for you to accumulate at least $1400.