Answer:
1 bright fringe every 33 cm.
Step-by-step explanation:
The formula to calculate the position of the m-th order brigh line (constructive interference) produced by diffraction of light through a diffraction grating is:
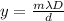
where
m is the order of the maximum
 is the wavelength of the light
is the wavelength of the light
D is the distance of the screen
d is the separation between two adjacent slit
Here we have:
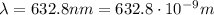 is the wavelength of the light
is the wavelength of the light
D = 1 m is the distance of the screen (not given in the problem, so we assume it to be 1 meter)
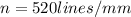 is the number of lines per mm, so the spacing between two lines is
is the number of lines per mm, so the spacing between two lines is

Therefore, substituting m = 1, we find:
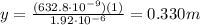
So, on the distant screen, there is 1 bright fringe every 33 cm.