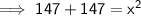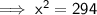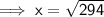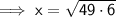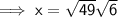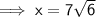Answer:
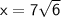
Explanation:
As the base angles of the triangle are the same, then the legs of the right triangle are also equal. Therefore, we can use Pythagoras' Theorem to calculate x.
Pythagoras' Theorem: a² + b² = c²
(where a and b are the legs, and c is the hypotenuse of the right triangle)
Given:
Substituting the given values into the formula: