Question

Find the exact length of side a

select a,b,c or d from the pictures, please help!

Answer 1

`a=2√(3)`

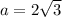
Explanation:

Side a is the side opposite angle A.

Side b is the side opposite angle B.

Side c is the side opposite angle C.

We have been given the lengths of 2 sides and the included angle.

Therefore, to find side a use the cosine rule.

Cosine rule

`a^2=b^2+c^2-2bc \cos A`

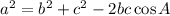
where:

• a, b and c are the sides
• A is the angle opposite side a

From inspection of the triangle:

• side b = 2
• side c = 4
• angle A = 60°

Substitute the given values into the formula and solve for a:

`\implies a^2=b^2+c^2-2bc \cos A`

`\implies a^2=2^2+4^2-2(2)(4) \cos 60^(\circ)`

`\implies a^2=4+16-16\left((1)/(2)\right)`

`\implies a^2=4+16-8`

`\implies a^2=12`

`\implies a=√(12)`

`\implies a=√(4 \cdot 3)`

`\implies a=√(4)√(3)`

`\implies a=2√(3)`

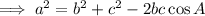
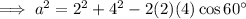
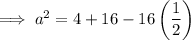
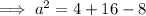
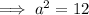
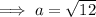
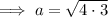
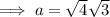
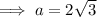
Therefore, the exact length of side a is 2√3.

Answer 2

• D. 2√3

Explanation:

The given triangle is right because the side adjacent to 60° angle is half the length of the hypotenuse.

Side a = BC is opposite to ange A, its measure is:

• BC/AC = √3
• BC = AC√3
• BC = 2√3

Correct choice is D