Answer:
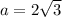
Explanation:
Side a is the side opposite angle A.
Side b is the side opposite angle B.
Side c is the side opposite angle C.
We have been given the lengths of 2 sides and the included angle.
Therefore, to find side a use the cosine rule.
Cosine rule
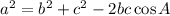
where:
- a, b and c are the sides
- A is the angle opposite side a
From inspection of the triangle:
- side b = 2
- side c = 4
- angle A = 60°
Substitute the given values into the formula and solve for a:
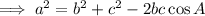
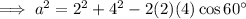
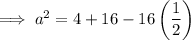
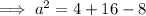
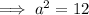
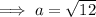
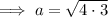
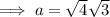
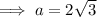
Therefore, the exact length of side a is 2√3.