The length of GM is 16. It is obtained from the right triangle KMI, altitude IG is drawn to hypotenuse KM and KG = 9 and IG= 12.
Explanation:
The given is,
Right triangle KMI
KG = 9
IG= 12
Step:1
From the triangle KMI,
90° = ∅
 + ∅
+ ∅
 .................................(1)
.................................(1)
From the triangle KGI,
Trignometric ratio,
tan ∅
 =
=
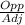 .................................(2)
.................................(2)
Where, Opp = 9
Adj = 12
Equation (2) becomes,
tan ∅
 =
=
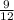
= 0.75
∅
 =
=
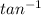 0.75
0.75
∅
 = 36.87°
= 36.87°
From the equation (1),
∅
 = 90° - ∅
= 90° - ∅

= 90° - 36.87°
∅
 = 53.13°
= 53.13°
From the triangle IGM,
tan ∅
 =
=
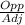 ..........................(3)
..........................(3)
Where, Opp = GM
Adj = 12
∅
 = 53.13°
= 53.13°
Equation (2) becomes,
tan 53.13° =

GM = (1.333)(12)
= 15.999
GM ≅ 16
Result:
The length of GM is 16. It is obtained from the right triangle KMI, altitude IG is drawn to hypotenuse KM and KG = 9 and IG= 12.