Question

Cone W has a radius of 6 cm and a height of 5 cm. Square pyramid X has the same base area and height as cone W.

Paul and Manuel disagree on the reason why the volumes of cone W and square pyramid X are related. Examine their arguments. Which statement explains whose argument is correct and why?

Answer 1

Manuel is correct. Paul used the incorrect base area.

Explanation:

If we calculate using the equation: 1/3 x pi x r^2 x h, and the plug in 3.14 for pi, 6 for radius, and 5 for height, we can get 188.4.

In that case, we can eliminate the two choices where it says Paul is correct. Now, if we take a closer look at the formulas of the base, we can see that Paul used diameter instead of radius to calculate the base area, which in turn, would turn out to be incorrect.

Therefore, Manuel is correct and Paul used the incorrect base area.

Answer 2

Manuel's argument is correct. Paul used the incirrect base area to find the volume of square pyramid X

Explanation:

step 1

Find the volume of the cone W

we know that

The volume of the cone if given by the formula

`V=(1)/(3)\pi r^(2) h`

we have

`r=6\ cm\\h=5\ cm`

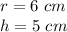
substitute the given values

`V=(1)/(3)\pi (6)^(2) (5)`

`V=60\pi\ cm^3`

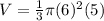
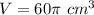
assume

`\pi=3.14`

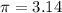
substitute

`V=60(3.14)=188.4\ cm^3`

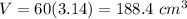
step 2

Find the volume of the square pyramid

we know that

The volume of the pyramid is given by the formula

`V=(1)/(3)Bh`

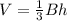
where

B is the area of the base

h is the height of pyramid

In this problem we have that

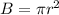`B=\pi r^2` ----> is the same that the area of the base of cone

so

`B=3.14(6^2)=113.04\ cm^2`

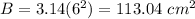
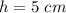`h=5\ cm` ----> is the same that the height of the cone

so

substitute

`V=(1)/(3)(113.04)(5)=188.4\ cm^3`

therefore

Manuel's argument is correct. Paul used the incirrect base area to find the volume of square pyramid X