Question

How many solutions does a triangle with side lengths a = 4, A = 112º and b =
9 have?​

Answer 1

There are 0 solutions.

Explanation:

Take note that since a<b, there are 3 possibilities (b/a)sinA is less than, equal to, or greater than 1.

When I solved for (9/4)sin(112degrees) I got about 2.09, which is greater than 1. The rule is that if it is greater than one, there are no solutions. So 0 is the answer.

Answer 2

This case has NO solutions.

Explanation:

Notice that you are in a case of an obtuse triangle (one of its angles is larger than 90 degrees), the side opposite to the obtuse triangle is shorter than the side adjacent to the angle, so no actual triangle can be formed.

This can be found by simply trying to apply the Law of Sines to solve for the value of angle "B" opposite to side "b":

`(sin(A))/(a) =(sin(B))/(b)\\sin(B)=(b\,sin(A))/(a)\\sin(B)=(9\,sin(112^o))/(4)\\\\sin(B)=2.086`

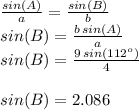
As shown above, we get an impossible mathematical condition (also call an absurd), since the sine of an angle cannot give a value larger than 1 (one).

Therefore, there is no angle we can find to build a triangle with the given data.