Question

Solving exponential equations with a common base problem in the picture!

Answer 1

Given:

The given expression is
`18^{x^(2)+4 x+4}=18^(9 x+18)`

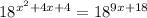
We need to determine the solution of the given expression.

Solution:

Let us solve the exponential equations with common base.

Applying the rule, if
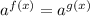`a^(f(x))=a^(g(x))` then
`f(x)=g(x)`

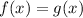
Thus, we have;

`x^(2)+4 x+4=9 x+18`

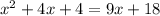
Subtracting both sides of the equation by 9x, we get;

`x^(2)-5 x+4=18`

Subtracting both sides of the equation by 18, we have;

`x^(2)-5 x-14=0`

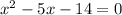
Factoring the equation, we get;

`x^2-7x+2x-14=0`

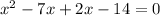
Grouping the terms, we have;

`(x^2-7x)+(2x-14)=0`

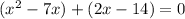
Taking out the common term from both the groups, we get;

`x(x-7)+2(x-7)=0`

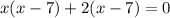
Factoring out the common term (x - 7), we get;

`(x+2)(x-7)=0`

`x+2=0 \ and \ x-7=0`

`x=-2 \ and \ x=7`

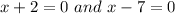
Thus, the solution of the exponential equations is x = -2 and x = 7.

Hence, Option C is the correct answer.