Question

"D" size batteries produced by MNM Corporation have had a life expectancy of 85.8 hours. Because of an improved production process, the company believes that there has been an INCREASE in the life expectancy of its D size batteries. A sample of 54 batteries showed an average life of 88.7 hours with a standard deviation of 3.8 hours. Conduct an appropriate hypothesis test. Find the t-statistic and the appropriate conclusion at the 0.1 level of significance.

Answer 1

The calculated value t = 5.608 > 2.3988 at 0.1 level of significance with 53 degrees of freedom.

The null hypothesis is rejected at 0.1 level of significance

The company do not believes that there has been an INCREASE in the life expectancy of its D size batteries

Explanation:

Step(i):-

Given data the size of sample n=54

Given "D" size batteries produced by MNM Corporation have had a life expectancy of 85.8 hours

therefore mean of Population μ = 85.5 hours

Given a sample of 54 batteries showed an average life of 88.7 hours with a standard deviation of 3.8 hours

The mean of the sample x⁻ = 88.7 hours

The standard deviation of the sample (S) = 3.8 hours

Step(ii):-

Null hypothesis : H₀:μ > 85.5 hours

Alternative hypothesis: H₁:μ < 85.5 hours

Level of significance : ∝= 0.1

Degrees of freedom γ =n-1 = 54-1 =53

The test statistic

`t= (x^(-)-u )/((S)/(√(n) ) )=(88.7-85.8)/((3.8)/(√(54) ) )`

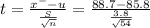
t = 5.608

The tabulated value t = 2.3988 at 0.1 level of significance with 53 degrees of freedom.

Conclusion:-

The calculated value t = 5.608 > 2.3988at 0.1 level of significance with 53 degrees of freedom.

The null hypothesis is rejected at 0.1 level of significance

The company do not believes that there has been an INCREASE in the life expectancy of its D size batteries