The length and width of the rectangle is 11 in and 8 in respectively.
Explanation:
Given,
The width of a rectangle is 3 in less than the length.
The area of each congruent right angle triangle = 44 in²
To find the length and width of the rectangle.
Formula
The area of a triangle with b base and h as height =
 bh
bh
Now,
Let, the width = x and the length = x+3.
Here, for the triangle, width will be its base and length will be its height.
According to the problem,
 ×(x+3)×x = 44
×(x+3)×x = 44
or,
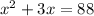
or,

or,
 +(11-8)x-88 = 0
+(11-8)x-88 = 0
or,
 +11x-8x-88 =0
+11x-8x-88 =0
or, x(x+11)-8(x+11) = 0
or, (x+11)(x-8) = 0
So, x = 8 ( x≠-11, the length or width could no be negative)
Hence,
Width = 8 in and length = 8+3 = 11 in