Answer:
The fifth degree Taylor polynomial of g(x) is increasing around x=-1
Explanation:
Yes, you can do the derivative of the fifth degree Taylor polynomial, but notice that its derivative evaluated at x =-1 will give zero for all its terms except for the one of first order, so the calculation becomes simple:
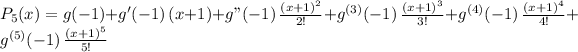
and when you do its derivative:
1) the constant term renders zero,
2) the following term (term of order 1, the linear term) renders:
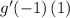 since the derivative of (x+1) is one,
since the derivative of (x+1) is one,
3) all other terms will keep at least one factor (x+1) in their derivative, and this evaluated at x = -1 will render zero
Therefore, the only term that would give you something different from zero once evaluated at x = -1 is the derivative of that linear term. and that only non-zero term is:
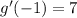 as per the information given. Therefore, the function has derivative larger than zero, then it is increasing in the vicinity of x = -1
as per the information given. Therefore, the function has derivative larger than zero, then it is increasing in the vicinity of x = -1