Question

If 10 friends are going to occupy 10 seats in shuttle on the way to the airport, how many different ways can they arrange themselves in the shuttle?

Answer 1

The number of different ways 10 friends can arrange themselves in a shuttle with 10 seats is 3,628,800.

Step-by-step explanation:

In this case, we have 10 friends who need to occupy 10 seats in a shuttle. The number of different ways they can arrange themselves can be calculated using the concept of permutations. Since each friend can occupy any of the 10 seats, we have 10 choices for the first seat, 9 choices for the second seat, 8 choices for the third seat, and so on. Therefore, the total number of different ways they can arrange themselves is 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1, which is equal to 3,628,800.

Answer 2

3,628,800 ways can they arrange themselves in the shuttle, If 10 friends are going to occupy 10 seats in shuttle on the way to the airport.

Step-by-step explanation:

The given is,

10 friends are going to occupy 10 seats in shuttle on the way to the airport

Step:1

No. of friends - 10

No.of seats in space shuttle - 10

Formula to calculate the no. of ways to arrange,

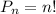`P_(n) = n!`............................(1)

Where, n - Positive integer

Step:2

From given, n = 10

Equation (1) becomes,

`P_(10) = 10!`

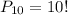
= 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1

= 3628800

= 3628800 ways

Result:

3,628,800 ways can they arrange themselves in the shuttle, If 10 friends are going to occupy 10 seats in shuttle on the way to the airport.