Question

Atire company finds the lifespan for one brand of its tires is normally distributed with a mean of 50,000 miles and a standard deviation of 4,000 miles. What is the Z-score for a tire lasting 52,000

miles?
0.96
0.88
0.50
25

Answer 1

Option C) 0.50 is the Z-score for a tire lasting 52,000 miles.

Explanation:

The z-core is the value decreased by the mean, divided by the standard deviation.

The formula to calculate the z-score value is given by,

`z =(x-mean)/(SD)`

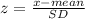
It is given that,

• The mean is 50,000 miles and standard deviation is 4,000 miles.
• We need to find out the Z-score for a tire lasting 52,000 miles.

Therefore the x value is 52000. Now, substitute the following in z-score formula,

• x = 52,000 miles
• Mean = 50,000 miles
• SD = 4,000 miles

⇒ z-score = (52000 - 50000) / 4000

⇒ z-score = 0.50

∴ Option C) 0.50 is the Z-score for a tire lasting 52,000 miles.