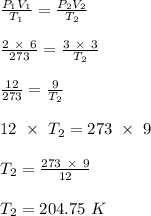The new temperature of the sample of gas, given that the pressure increases to 3.00 atm is 204.75 K
How to calculate the new temperature of the gas?
A good look a the question given above, shows that the new temperature of the sample of gas can be calculated using the combined gas equation. This is shown below:
- Initial temperature of gas sample (T₁) = 2732 K
- Initial pressure of gas sample (P₁) = 2.00 atm
- Initial volume of gas sample (V₁) = 6.00 liters
- New volume of gas sample (V₂) = 3.00 liters
- New pressure of gas sample (P₂) = 3.00 atm
- New temperature of gas sample(T₂) = ?