Answer:
Domain: all real numbers
Range: all real numbers
Explanation:
I'm assuming you mean the function
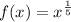 . That's usually written
. That's usually written
f(x) = x^(1/5) with the ^ meaning "to the power of..." and the fraction exponent in parentheses so as not to be confused with x^1/5 which could mean x to the first power, divided by 5.
Fractional exponents are used to indicate roots. In this case, x is being raised to the 1/5 power, so this is the fifth root of x, written
![\sqrt[5]{x}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/bif0epm5pqfgtb592xzx130zjtcmg4l18d.png) . The 5 is called the root index.
. The 5 is called the root index.
For odd roots, like this one, the domain is all real numbers--x can be any number at all. So the domain is all real numbers.
The range is also all real numbers. Attached is a graph of this function. It might not look like it, but the graph rises to the right to any height. The larger x gets, the larger the 5th root gets. A similar thing happens on the left--the smaller x gets, the smaller the 5th root gets.
EDIT: see the comment. For the function
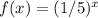 , the domain is all real numbers. The range is positive real numbers. I'll attach a graph!
, the domain is all real numbers. The range is positive real numbers. I'll attach a graph!