Question

Erlinda is having a party and wants to fill her hot tub. If she only uses the red hose, it takes 3 hours more than if she only uses the green hose. If she uses both hoses together, the hot tub fills in 2 hours. How long does it take for each hose to fill the hot tub?

Answer 1

The red hose would take 6 hours alone, and the green hose would take 3 hours alone to fill the hot tub.

Explanation:

0=(x−3)(x+2)

x−3= 0, x+2=0

x=3

3+3 . 3

6 hours 3 hours

Answer 2

Green hose takes 3 hours to fill her hot tub and Red hose takes 6 hours to fill her hot tub.

Explanation:

The given is,

Red hose takes 3 hours more than if she only use green hose

She uses both hoses together, the hot tube fills in 2 hours

Step:1

Let, x - Hours taken by green hose to fill her tub

From given,

Time taken by red hose = (x + 3) Hours

Time taken by both hoses = 2 hours

One hour work,

One hour work of green hose =
`(1)/(x)`

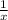
One hour work of Red hose =
`(1)/(x+3)`

One hour work both hoses uses together =
`(1)/(2)`

One hour work if she use both hoses together

= One hour work of green hose + One hour work of red hose

`(1)/(2) = ((1)/(x) +(1)/(x+3) )`

`(1)/(2) = (x+x+3)/((x+3)(x))`

`(1)/(2) = (2x+3)/((x^(2) +3x))`

`x^(2) +3x = 2(2x+3)`

`x^(2) + 3x = 4x+6`

`x^(2) -x-6=0`

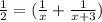
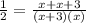
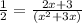
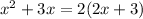
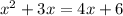
Solving the above equation,

x = 3

From the x value,

Hours taken by green hose to fill her tub, x = 3 hours

Time taken by red hose = (x + 3) Hours

= 3 + 3 = 6 hours

Hours taken by Red hose to fill her tub = 6 hours

Result:

Green hose takes 3 hours to fill her hot tub and Red hose takes 6 hours to fill her hot tub.