Answer:
a. $408,334.39
b. $3,457.40
Step-by-step explanation:
r = rate per period = 8% = 0.08
P = Initial Value of Gift = $10,000
t = time = 30 - 5 = 25, As received after 5 years.
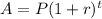
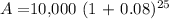
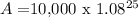
A = $10,000 x 6.8485
A = $68,484.75
![FV of annuity = P [((1 + r)^(n) - 1)/(r) ]](https://img.qammunity.org/2021/formulas/business/college/jjihtx0gxy93ug6zlix1rf4p65jndk0jst.png)
P = Periodic Payment = $3,000
a.
n = number of periods = 30
![FV of annuity = 3,000 [((1 + 0.08)^(30) - 1)/(0.08) ]](https://img.qammunity.org/2021/formulas/business/college/2k9923wq6xn6olq72kd98lulzb6bnn9rt0.png)
![FV of annuity = 3,000 [((1.08)^(30) - 1)/(0.08) ]](https://img.qammunity.org/2021/formulas/business/college/76i8hxu0cbmmk3461bazg9xl1lrdouuc0r.png)
![FV of annuity = 3,000 [\frac{10.0627 - 1} {0.08} ]](https://img.qammunity.org/2021/formulas/business/college/zpk9n59qq6c23432x63ucvs9dzdri667uq.png)
![FV of annuity = 3,000 [\frac{9.0627} {0.08} ]](https://img.qammunity.org/2021/formulas/business/college/w5sq0nc6t70b6qrqr33p5gum3hkptjivcs.png)
FV of annuity = $3,000 x 113.2832
FV of annuity = $339,849.63
Accumulated value of money can be calculated as follows;
$68,484.75 + $339,849.63
$408,334.39
b.
If they wish to retire with $800,000 savings, they need to save additional amount of money every year to provide additional amount of money, as follows;
$800,000 - $68,484.75
$731,515.24
The extra annual savings can be calculated as follows;
![731,515.24 = P [((1 + 0.08)^(30) - 1 )/(0.08) ]](https://img.qammunity.org/2021/formulas/business/college/7h5xbh7ude3siqi9sra64cw03pexh4j9qu.png)
$731,515.24 = P x 113.28
Divide the above equation by 113.28 we get;
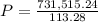
P = $6,457.40
They are already paying $3,000, So the extra saving they need make every year is calculated as follows;
$6,457.40 - $3,000
$3,457.40