Question

A computer cooled by a fan contains eight PCBs, each dissipating 10W power. The height of the PCBs is 12 cm and the length is 18 cm. The cooling air is supplied by a 25 W fan mounted at the inlet. If the temperature rise of air as it flows through the case of the computer is not to exceed 10 C, determine (a) the flow rate of the air that the fan needs to deliver and (b) the fraction of the temperature rise of air that is due to the heat generated by the fan and its motor.

Answer 1

a) The flow rate of the air is 0.0104 kg/s

b) The fraction of the temperature is 23.91%

Step-by-step explanation:

a) Given:

N = Number of PCBs = 8

Q = heat dissipated = 10 W

W = power supplied = -25 W

ΔT = rise temperature = 10°C

The total amount of heat dissipated is equal to:

`Q_(T) =N*Q=8*10=80W`

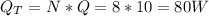
The expression of conservation of energy is:

`E_(in) =E_(out) \\Q_(T) +m_(in) h_(in) =m_(out) h_(out) +W\\m_(in)=m_(out) m_(air),(mass-balance)\\Q_(T)=m_(air)(h_(out) -h_(in))+W\\h=CpT\\Q_(T)=m_(air)Cp(T_(out) -T_(in))+W`

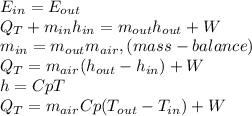
Replacing:

`80=m_(air) *1.005x10^(3) *10+(-25)\\m_(air) =0.0104kg/s`

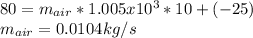
b) The amount of heat is equal:

`Q_(fan) =m_(air) Cp*delta-T\\25=0.0104*1.005x10^(3) *delta-T\\delta-T=2.391C`

The fraction of the temperature is:

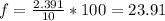`f=(2.391)/(10) *100=23.91`%