Question

Suppose that a wing component on an aircraft is fabricated from an aluminum alloy that has a plane strain fracture toughness of 27 MPa (24.57 ksi). It has been determined that fracture results at a stress of 115 MPa (16680 psi) when the maximum internal crack length is 8.3 mm (0.3268 in.). For this same component and alloy, compute the stress level at which fracture will occur for a critical internal crack length of 5.9 mm (0.2323 in.).

Answer 1

The stress level = 133.5 Mpa

Step-by-step explanation:

Given data;

Toughness = 27Mpa

Stress = 115 Mpa

Crack length = 8.3mm = 8.3 * 10^-3m

The stress level can be calculated using the formula,

б =
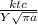`(ktc)/(Y√(\pi a) )` ---------------------------------------------1

Where;

б = strain level

ktc = fracture toughness

a = surface length = 8.3 *10^-3/2 (Half of the cracked length)

Substituting into the formula, we have

But, we have to calculate the parameter Y before we can substitute into equation 1.

By making Y subject formula, we have;

Y = ktc/ (б√πa)

Y = 27/(115 *√(π * (8.3 *10^-3/2))

Y = 27/(115 *√0.0130)

Y = 27/(115 * 0.114)

Y = 27/13.131

Y = 2.1

Calculating the stress level, we substitute into equation 1 as follows;

б =
`(ktc)/(Y√(\pi a) )`

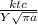
б = 27/ (2.1 *√(π * (5.9 * 10^-3/2))

= 27/(2.1 *√(π * 0.00295))

= 27/ (2.1 *√0.00927)

= 27/(2.1 * 0.096)

= 27/0.202

= 133.5 Mpa