Answer:
a)
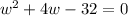 is the equation to determine the width of rectangle.
is the equation to determine the width of rectangle.
b) Length of rectangle is
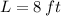 and width of rectangle is
and width of rectangle is

Explanation:
Part a:
Given that the landscaper is rectangular in shape. So to find the equation of width use area formula for rectangle.
Formula for area of rectangle,
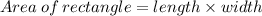
To find the length and width, it is given that length is 4 feet longer than width that is,
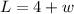
Also, Area is
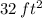 .
.
Substituting the values,

Using distributive property and simplifying,
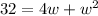
Subtracting 32 from both sides,
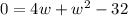
Rewriting it in form of
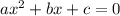 ,
,
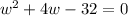
So, the equation in standard form which is used to determine the width of rectangle is
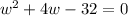
Part b:
To solve the above equation use the quadratic formula,

Rewriting it in terms of w,
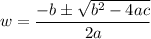
where, a = 1, b = 8 and c = - 32.
Substituting the values,
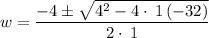
Simplifying,
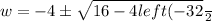
Applying rule,
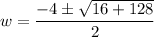
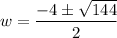
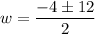
Hence there are two values of x as follows,
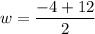 and
and
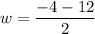
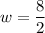 and
and
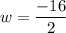
 and
and
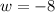
Since value of width cannot be negative so,

Now using
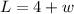 to find the length.
to find the length.
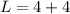
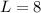
Therefore, length and width of rectangle is
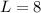 and
and
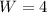 respectively.
respectively.