Answer:
- Balanced chemical reaction:
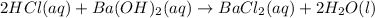
- Concentration of the initial barium hydroxide solution:
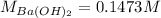
- Concentrations of barium and chloride ions:
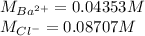
Step-by-step explanation:
Hello,
In this case, the balanced chemical reaction with the proper physical states is:
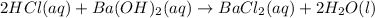
Moreover, it is convenient to perform the titration analysis in terms of normalities, therefore, HCl's normality becomes equal to its molarity as it is monoprotic (only one hydrogen in its formula), thus, we find barium hydroxide's normality:
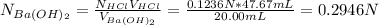
Hence, for the molarity, since two hydroxiles are in the barium hydroxide, 2 grams-equivalents are 1 mole, thus, its molarity is:
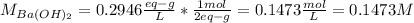
Then, after mixing and carry out the neutralization reaction the resulting volume is:
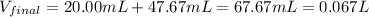
In addition, the moles of both barium and chloride ions are:
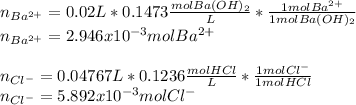
Finally, the concentrations of such ions are:
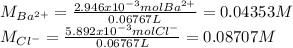
Best regards.