Question

A 20.00 mL Ba(OH)_2 solution of unknown concentration was neutralized by the addition of 47.67 mL of a 0.1236 M HCl solution. Write the balanced molecular equation for the neutralization reaction between HCl and Ba(OH)_2 in aqueous solution. Include physical states. 2HCl(aq) + Ba(OH)_2(aq) rightarrow BaCl_2(aq) + 2H_2O(l) Calculate the concentration of Ba(OH)_2 in the original 20.00 mL solution Calculate the concentrations of Ba^2+ and Cl^- in solution following the neutralization reaction.

Answer 1

The concentration of Ba(OH)₂ is 0.147 M

The concentration of Ba²⁺ is 0.043 M

The concentration of Cl⁻¹ is 0.087 M

Step-by-step explanation:

The concentration of Ba(OH)₂ is:

`M_{Ba(OH)_(2) } =(M_(HCl)*V_(HCl) )/(2*V_(sol) )`

Where

MHCl = 0.1236 M

VHCl = 47.67 mL

Vsol = 20 mL

Replacing:

`M_{Ba(OH)_(2) } =(0.1236*47.67)/(2*20) =0.147M`

The concentration of Ba²⁺ is:

`[Ba^(2+) ]=\frac{V_(sol)*V_{Ba(OH)_(2) }}{V_(sol)+V_(HCl)} =(20*0.147)/(20+47.67) =0.043M`

The concentration of Cl⁻¹ is:

`[Cl^(-1) ]=(V_(HCl)*M_(HCl ))/(V_(sol)+V_(HCl)) =(47.67*0.1236)/(20+47.67) =0.087M`

Answer 2

- Balanced chemical reaction:

`2HCl(aq) + Ba(OH)_2(aq) \rightarrow BaCl_2(aq) + 2H_2O(l)`

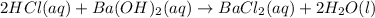
- Concentration of the initial barium hydroxide solution:

`M_(Ba(OH)_2)=0.1473M`

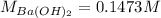
- Concentrations of barium and chloride ions:

`M_(Ba^(2+))=0.04353M\\M_(Cl^-)=0.08707M`

Step-by-step explanation:

Hello,

In this case, the balanced chemical reaction with the proper physical states is:

`2HCl(aq) + Ba(OH)_2(aq) \rightarrow BaCl_2(aq) + 2H_2O(l)`

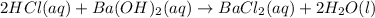
Moreover, it is convenient to perform the titration analysis in terms of normalities, therefore, HCl's normality becomes equal to its molarity as it is monoprotic (only one hydrogen in its formula), thus, we find barium hydroxide's normality:

`N_(Ba(OH)_2)=(N_(HCl)V_(HCl))/(V_(Ba(OH)_2))=(0.1236N*47.67mL)/(20.00mL)=0.2946N`

Hence, for the molarity, since two hydroxiles are in the barium hydroxide, 2 grams-equivalents are 1 mole, thus, its molarity is:

`M_(Ba(OH)_2)=0.2946(eq-g)/(L)*(1mol)/(2eq-g)=0.1473(mol)/(L)=0.1473M`

Then, after mixing and carry out the neutralization reaction the resulting volume is:

`V_(final)=20.00mL+47.67mL=67.67mL=0.067L`

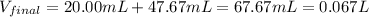
In addition, the moles of both barium and chloride ions are:

`n_(Ba^(2+))=0.02L*0.1473(molBa(OH)_2)/(L) *(1molBa^(2+))/(1molBa(OH)_2) \\n_(Ba^(2+))=2.946x10^(-3)mol Ba^(2+)\\\\n_(Cl^-)=0.04767L*0.1236(molHCl)/(L) *(1molCl^-)/(1molHCl) \\n_(Cl^-)=5.892x10^(-3)mol Cl^-`

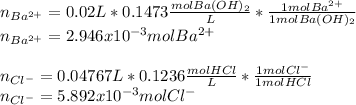
Finally, the concentrations of such ions are:

`M_(Ba^(2+))=(2.946x10^(-3)molBa^(2+))/(0.06767L)= 0.04353M\\M_(Cl^-)=(5.892x10^(-3)molCl^-)/(0.06767L)= 0.08707M`

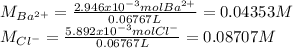
Best regards.