Answer:
6.598
Explanation:
- A random sample of n = 1,045 young adults found that 60 % do not have a landline telephone number.
- We have to test the hypothesis that whether the data provide statistical evidence that more than 50 percent of all young adults do not have a landline telephone number.
- Let Null Hypothesis, H_o: p 0.50
- Alternate Hypothesis, H_1 : p > 0.50
- The test statistics that will be used here is One-sample proportion test;
Test =
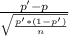 ~ N(0,1)
~ N(0,1)
- Where, p' = % of young adults who do not have a landline telephone number in a sample of n is = 60%
- Where, n = sample of young adults = 1,045
- So, test statistics =
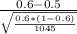 = 6.598
= 6.598
- Hence, the test statistic for the test is 6.598.