Answer:
Therefore the bank need to offer 23.6% annual interest rate compounded twice.
Explanation:
Compound interest formula:
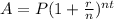
A=Amount
P=Principal
r=rate of interest
n= Number of times interest is compounded per year.
t= time
Bank A
P=$55,000, r=25% = 0.25, n=1, t=t
The amount that the school have to pay after t year is

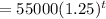
Bank B
P=$55,000, r=?, n=2, t=t
The amount that the school have to pay after t year is
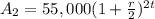
Since the amount for both banks are same.
i.e

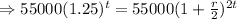

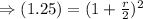
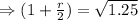
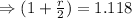
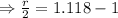
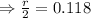
⇒r=0.118×2
⇒r = 0.236
⇒r =23.6%
Therefore the bank need to offer 23.6% annual interest rate compounded twice.