Answer:
the coordinates of the vertex are: (2.5, -24.5)
Explanation:
Recall that when we have a quadratic in its standard form:

the position of the x-coordinate for the vertex can be obtained via:
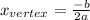
Then in order to find the vertex, first we write the expression in standard form:
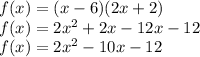
Now that we have the values for the parameters "
 " and "b" we find the x of the vertex:
" and "b" we find the x of the vertex:
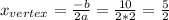
Now we use this x-value in the function to find the correspondent y-value of the vertex:
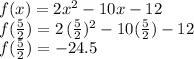
Then, the coordinates of the vertex are: (2.5, -24.5)