Question

PLEASE HELP!!
Solve x^2=81 and x^2-18x=7.
Please show your work!

Answer 1

x² = 81 , x = ± 9

x² - 18x = 7 : x = 9 ± √(22)

Explanation:

x² = 81

simply take the square root of both sides

x = ± 9

x² - 18x = 7

This question is a bit more complicated as there is a variable with a power as well as a variable with no power. To solve for x we are going to have to put the equation in quadratic form then solve using the quadratic equation

x² - 18x = 7

put the equation in quadratic form by subtracting 7 from both sides so that the equation is equal to 0

x² - 18x - 7 = 0

we can now solve for x using the quadratic equation

recall the quadratic equation :
`x=(-b+√(b^2-4ac) )/(2a)`

where the value of a,b and c are derived from the equation

remember the equation is in quadratic form ax² + bx + c = 0

so ax² + bx + c = 0 : x² - 18x - 7 = 0

knowing this we can assign variables, a = 1 , b = -18 and c = -7

now we plug in the variables into the quadratic equation

recall equation :
`x=(-b+√(b^2-4ac) )/(2a)`

a = 1 , b = -18 and c = -7

plug in values

`x=(-(-18)+√((-18)^2-4(1)(-7)) )/(2(1))`

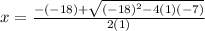
remove parenthesis

`x=(18+√((-18)^2-4(1)(-7)) )/(2(1))`

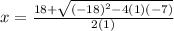
simplify exponent

`x=(18+√(324-4(1)(-7)) )/(2(1))`

simplify multiplication in square root and on denominator

`x=(18+√(324+28) )/(2)`

simplify addition

`x=(18+√(352) )/(2)`

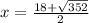
simplify radical

`x=(18+4√(22) )/(2)`

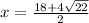
simplify fraction

`x=9+or-√(22)`

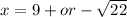
and we are done!