Question

For some viscoelastic polymers that are subjected to stress relaxation tests, the stress decays with time according to where σ(t) and σ(0) represents the time-dependent and initial (i.e., time =0) stresses, respectively, and t and τ denote elapsed time and the relaxation time; τ is a time-independent constant characteristic of the material. A specimen of some viscoelastic polymer with the stress relaxation that obeys Equation 7.40, was suddenly pulled in a tension to a measured strain of 0.5; the stress necessary to maintain this constant strain was measured as a function of time. Determine Er(8) for this material if the initial stress level was 2.62 MPa (380 psi), which dropped to 1.73 MPa (251 psi) after 64 s.

Answer 1

`E_r(8)` of the material is 4.98 MPa

Step-by-step explanation:

Consider the equation of stress decay for viscoelastic polymers

where; σ(t): 1.73 MPa , σ(0): 2.62 MPa , t: 64 s

σ(t) = σ(0)exp(-t/r)

1.73 = 2.62 exp(-64/r)

exp(-64/r) = 1.73 ÷ 2.62

exp(-64/r) = 0.6603

-64 / r = Ln 0.6603

-64 / r = -0.4151

-64 / -0.4151 = r

r = 154.18 s

Consider the equation of stress decay for viscoelastic polymers

σ(t) = σ(0)exp(-t/r)

substitute 8 s for t

σ(8) = (2.62)exp(-8/154.18)

Ln σ(8) = Ln(2.62) - 8/154.18

Ln σ(8) = 0.9632 - 0.051887

Ln σ(8) = 0.911313

σ(8) = 2.49 MPa

Consider the equation relaxation modulus
`E_r(8)`

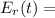`E_r(t) =` σ(t) / ε₀

Here, ε₀ is the strain level, which is maintained constant for σ(t) and ε₀ is the strain.

Substitute 0.5 for ε₀

`E_r(8)` = 2.49 MPa / 0.5

= 4.98 MPa

Therefore,
`E_r(8)` of the material is 4.98 MPa