Answer:
a) The maximum contact pressure is 274.58 MPa and the width of contact is 0.058 mm
b) The maximum shear stress is 82.37 MPa at a distance of 0.023 mm
Step-by-step explanation:
Given data:
L = 20 mm
F = 250 N
r₁ = 10 mm
r₂ = 15 mm
v = 0.3
E = 2.07x10⁵ MPa
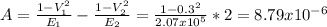
a) The maximum contact pressure is:
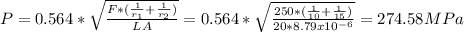
The width of contact is:
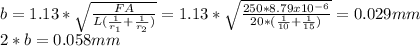
b) According the graph elastic stresses below the surface, for v = 0.3, the maximum shear stress is
T = 0.3*P = 0.3 * 274.58 = 82.37 MPa
At a distance of
0.8*b = 0.8*0.029 = 0.023 mm