Answer:
option e
Step-by-step explanation:
The avrami equation is given as follows
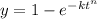
the above equation can be re-written as
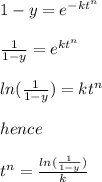
where y = the percentage
k = 4.46×10⁻⁴
t = time
n = constant
We determine n as follows
Using any of the cases, for instance case 1
when y = 40% or 0.4 , t = 13.1s
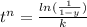
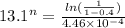
solving the above equation, we have
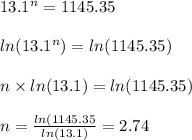
The value of n is the same if we use the second case
that is, y = 60% or 0.6 and t = 16.2s
Now when y = 95% or 0.95 and using n = 2.74
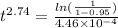
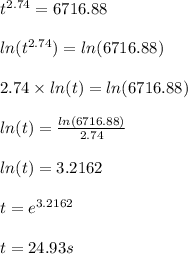
Hence
t = 25s