Question

In your first job with a large U.S based steel company, you have been assigned to a team tasked with developing a new low carbon steel alloy. In the iron-carbon system, the kinetics of the austenite to pearlite transformation obeys the Avrami relationship. In initial experimental data shows that the transformation reaches 40% completion in 13.1 seconds and 60% completion in 16.2 seconds, Determine the time (in seconds) required for the transformation in this new steel to reach 95% completion. Assume ak value of 4.46 x 104.

a. 90

b. 36.2

c. 45

d. 28

e. 25

Answer 1

option e

Step-by-step explanation:

The avrami equation is given as follows

`y = 1 -e^{-kt^(n) }`

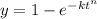
the above equation can be re-written as

`1-y = e^{-kt^(n) } \\\\(1)/(1-y) = e^{kt^(n)}\\\\ln((1)/(1-y) )=kt^(n) \\\\hence\\\\t^(n) = (ln((1)/(1-y) ))/(k)`

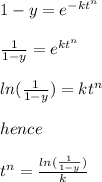
where y = the percentage

k = 4.46×10⁻⁴

t = time

n = constant

We determine n as follows

Using any of the cases, for instance case 1

when y = 40% or 0.4 , t = 13.1s

`t^(n) = (ln((1)/(1-y) ))/(k)`

`13.1^(n) = (ln((1)/(1-0.4) ))/(4.46* 10^(-4) )`

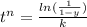
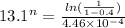
solving the above equation, we have

`13.1^(n) = 1145.35\\\\ln(13.1^(n)) = ln(1145.35)\\\\n* ln(13.1) = ln(1145.35)\\\\n = (ln(1145.35)/( ln(13.1))= 2.74`

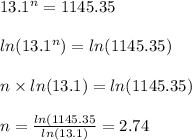
The value of n is the same if we use the second case

that is, y = 60% or 0.6 and t = 16.2s

Now when y = 95% or 0.95 and using n = 2.74

`t^(2.74) = (ln((1)/(1-0.95) ))/(4.46* 10^(-4) )`

`t^(2.74)= 6716.88\\ \\ln(t^(2.74))=ln(6716.88)\\\\2.74 * ln(t)=ln(6716.88)\\\\ln(t)=(ln(6716.88))/(2.74)\\ \\ln(t)=3.2162\\\\t = e^(3.2162)\\ \\t = 24.93s`

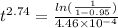
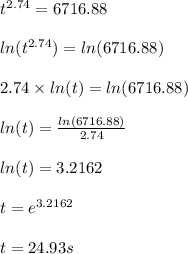
Hence

t = 25s

Answer 2

Option A

Step-by-step explanation: