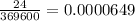Question

Three molecules of type A, three of type B, three of type C, and three of type D are to be linked together to form a chain molecule. One such chain molecule is ABCDABCDABCD, and another is BCDDAAABDBCC.

a.) How many such chain molecules are there?



[Hint: If the three A's were distinguishable from one another --A[1], A[2], A[3] and the B's and C's and D's were also how many molecules would be there be? How is the number reduced when the subscripts are removed from the A's?



B) Suppose a chain molecule of the type described is randomly selected. What is the probability that all three molecules of each type end up next to one another (such as in BBBAAADDDCCC)?

Answer 1

a) 369,600

b) 0.0000649

Explanation:

If all of the A's, B's, C's and D's were different, the number of ways to form a molecule would be calculated as n!. However, given that every molecule is repeat 3 times, we need to reduce the number dividing by 3! for every type of molecule.

It means that the number of ways in which we can organize n elements where not all of them are equal is calculated as:

`(n!)/(n_1!*n_2!*...*n_k!)`

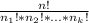
Where k is the number of elements that are differents and
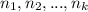`n_1,n_2,...,n_k` are the number of times that every element appears.

Now, we have 4 different types of molecules (A,B,C,D) so k is equal to 4. Additionally, there are 3 molecules of type A, 3 of type B, 3 of type C, and 3 of type D, so
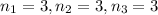`n_1=3, n_2=3, n_3=3` and
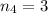`n_4=3`. It means that there are 369,600 ways to form chain molecules and it is calculated as:

`(12!)/(3!*3!*3!*3!)=369,600`

Now, the number of ways where all three molecules of each type end up next to one another is calculated as:

`4*3*2*1=24`

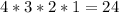
Because, first we have 4 possible types of molecules to occupy the first three positions, then we have 3 possible types of molecules to occupy the following 3 positions, then we have 2 possible types of molecules and finally we have 1 possible type of molecule

So, the probability that all three molecules of each type end up next to one another is calculated as:

`(24)/(369600)=0.0000649`