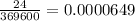Answer:
a) 369,600
b) 0.0000649
Explanation:
If all of the A's, B's, C's and D's were different, the number of ways to form a molecule would be calculated as n!. However, given that every molecule is repeat 3 times, we need to reduce the number dividing by 3! for every type of molecule.
It means that the number of ways in which we can organize n elements where not all of them are equal is calculated as:
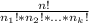
Where k is the number of elements that are differents and
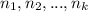 are the number of times that every element appears.
are the number of times that every element appears.
Now, we have 4 different types of molecules (A,B,C,D) so k is equal to 4. Additionally, there are 3 molecules of type A, 3 of type B, 3 of type C, and 3 of type D, so
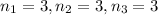 and
and
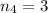 . It means that there are 369,600 ways to form chain molecules and it is calculated as:
. It means that there are 369,600 ways to form chain molecules and it is calculated as:
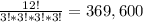
Now, the number of ways where all three molecules of each type end up next to one another is calculated as:
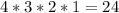
Because, first we have 4 possible types of molecules to occupy the first three positions, then we have 3 possible types of molecules to occupy the following 3 positions, then we have 2 possible types of molecules and finally we have 1 possible type of molecule
So, the probability that all three molecules of each type end up next to one another is calculated as: