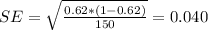Answer:
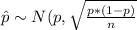
The estimated standard error is given by:
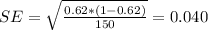
Explanation:
For this case we have the following data:
n =150 represent the sample size selected
x = 93 people stated that they always wear their seatbelt when they travel in a car
For this case the the proportion estimated is :
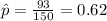
We can can check if we can use the normal approximation :
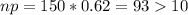
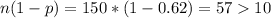
So then we can use the normal approximation and the distribution for the proportion is given:
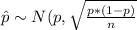
The estimated standard error is given by: