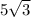Answer : The lengths of the other two sides of the triangle is, 5 and
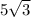
Step-by-step explanation :
Given:
∠ACB = 90°
∠CAB = 60°
∠ABC = 30°
Length of hypotenuse = 10
According to trigonometric function,
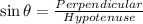
First we have to calculate the length AC.
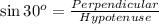
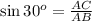
As we know that,
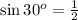
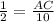
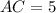
Now we have to calculate the length CB.
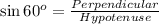
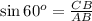
As we know that,
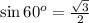
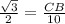
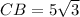
Therefore, the lengths of the other two sides of the triangle is, 5 and