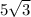Question

Triangle A B C is shown. Angle A C B is a right angle, angle C A B is 60 degrees, and angle A B C is 30 degrees. The length of the hypotenuse is 10.

What are the lengths of the other two sides of the triangle?

Answer 1

5/3

Explanation:

Answer 2

Answer : The lengths of the other two sides of the triangle is, 5 and
`5√(3)`

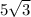
Step-by-step explanation :

Given:

∠ACB = 90°

∠CAB = 60°

∠ABC = 30°

Length of hypotenuse = 10

According to trigonometric function,

`\sin \theta=(Perpendicular)/(Hypotenuse)`

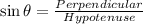
First we have to calculate the length AC.

`\sin 30^o=(Perpendicular)/(Hypotenuse)`

`\sin 30^o=(AC)/(AB)`

As we know that,
`\sin 30^o=(1)/(2)`

`(1)/(2)=(AC)/(10)`

`AC=5`

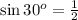
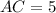
Now we have to calculate the length CB.

`\sin 60^o=(Perpendicular)/(Hypotenuse)`

`\sin 60^o=(CB)/(AB)`

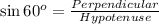
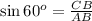
As we know that,
`\sin 60^o=(√(3))/(2)`

`(√(3))/(2)=(CB)/(10)`

`CB=5√(3)`

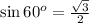
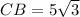
Therefore, the lengths of the other two sides of the triangle is, 5 and
`5√(3)`