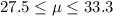Question

In a random sample of 27 people, the mean commute time to work was 30.4 minutes and the standard deviation was minutes. Assume the population is normally distributed and use a​ t-distribution to construct a ​% confidence interval for the population mean mu. What is the margin of error of mu​?

Answer 1

The 95% CI is

`27.5\leq \mu \leq 33.3`

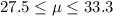
The margin of error is 2.9 minutes.

Explanation:

The question is incomplete:

The sample standard deviation was 7.3 minutes.

Assume the population is normally distributed and use a​ t-distribution to construct a ​95% confidence interval for the population mean mu.

The sample mean is 30.4

The sample standard deviation is 7.3

The sample size is 27.

The degrees of freedom are:

`df=n-1=27-1=26`

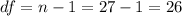
For a 95% CI and df=26, the critical value for t is t=2.056.

The margin of error can be calculated as:

`E=t\cdot s/√(n)=2.056*7.3/√(27)=15/5.2=2.9`

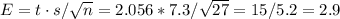
The lower and upper bounds of the 95% CI are:

`LL=\bar x-t\cdot s/√(n)=30.4-2.9=27.5\\\\UL=\bar x+t\cdot s/√(n)=30.4+2.9=33.3`

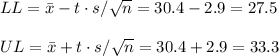
The 95% CI is then

`27.5\leq \mu \leq 33.3`