Answer:
The points that maximize the product xy on the circle x²+y²=18 are (3,3) and (-3,-3)
Explanation:
We have the function f(x,y) = xy, and we want to find its maximum with the restriction g(x,y) = 18; with g(x,y) = x²+y². The Lagrange multiplier theorem stays that a point (x,y) that is the maximum of f with the given restriction should fulfill the following:

Where
 is a constant. This means that there exists a constant
is a constant. This means that there exists a constant
Where, for a differentiable function h, h_x and h_y are the partial derivates of h respect to the variables x and y respectively. The partial derivate, for example with respect to the variable x, is obtained by derivating the function thinking the variable y as a constant.
With this in mind lets compute the partial derivates of f and g:
So, if we replace each partial derivate by its formula in the relations we had before, and we add the restriction g(x,y) = 18, we obtain the following 3 conditions:
Since
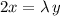 , then
, then
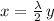 . If we replace the value of x in the other equation, we obtain that
. If we replace the value of x in the other equation, we obtain that
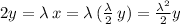
This means that
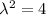 , thus
, thus
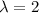 or
or
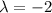 . We can translate both equations therefore as:
. We can translate both equations therefore as:
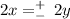

Thus, y = x, or y = -x. In order for xy to be positive (and hence, have a chance to be a maximum), we will only care about x=y.
Lets replace y with x in the restriction given by gi:
g(x,x) = 18
x²+x² = 2x² = 18
x² = 9
x = 3 or x = -3
Therefore, the candidates for maximum for f with the restriction g(x,y) = 18 are (3,3) and (-3,-3). In both cases f(x,y) = 3*3 = (-3)*(-3) = 9. As a result, both points maximize the product xy on the circle.