Question

Calculate the induced electric field in a 50-turn coil with a diameter of 15 cm that is placed in a spatially uniform magnetic field of magnitude 0.50 T so that the face of the coil and the magnetic field are perpendicular. This magnetic field is reduced to zero in 0.10 seconds. Assume that the magnetic field is cylindrically symmetric with respect to the central axis of the coil.

Answer 1

9.375 V/m

Step-by-step explanation:

number of turns, N = 50

diameter of the coil, 2r = 15 cm

r = 7.5 cm = 0.075 m

magnetic field, B = 0.5 T

final magnetic field, B' = 0 T

time required, t = 0.1 s

flux, Ф = N B A Cos 0°

`(d\phi)/(dt)=NA(dB)/(dt)`

`(d\phi)/(dt)=50* \pi r^(2)* (0-0.5)/(0.1)`

`(d\phi)/(dt)=-250* \pi r^(2)`

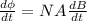
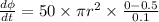
According to the Maxwell's equation

`\oint \overrightarrow{E}.d\overrightarrow{l}=-(d\phi)/(dt)`

`E* 2\pi r = 250 * \pi* r^(2)`

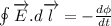
E = 125 x r

E = 125 x 0.075

E = 9.375 V/m

Thus, the electric field is 9.375 V/m.