Answer:
Length of beam = 10in
Step-by-step explanation:
We first calculate the maximum shear force.
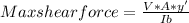
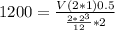
Calculating for V, we have:
V = 3200Ib
P = 3200 *2
P = 6.4k
Let's now use the equation for the load for a length.
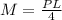

Using the stress equation,
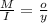
Inputting figures in the equation, we have:
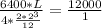
Solving for L, we have:
L = 10in
Length of beam will = 10in