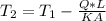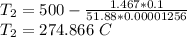Answer:
In Btu:
Q=0.001390 Btu.
In Joule:
Q=1.467 J
Part B:
Temperature at midpoint=274.866 C
Step-by-step explanation:
Thermal Conductivity=k=30 (Btu/hr)/(ft ⋅ °F)=
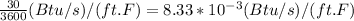
Thermal Conductivity is SI units:
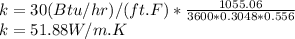
Length=20 cm=0.2 m= (20*0.0328) ft=0.656 ft
Radius=4/2=2 mm =0.002 m=(0.002*3.28)ft=0.00656 ft
T_1=500 C=932 F
T_2=50 C= 122 F
Part A:
In Joules (J)
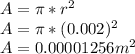
Heat Q is:
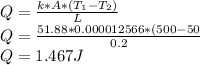
In Btu:
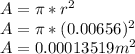
Heat Q is:
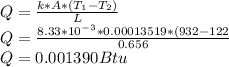
PArt B:
At midpoint Length=L/2=0.1 m
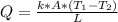
On rearranging: