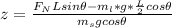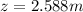Question

Sally wants to hang up some decorations on the side of her house, so she props up a ladder of length L = 3m against a wall at an angle of θ = 50° with respect to the horizontal. The ground is somewhat icy, where the coefficient of static friction between the ground and the ladder’s feet is µ = 0.55; while the wall of her house can be considered frictionless. If Sally has a mass of 60kg and the ladder has a mass of 80kg, what is the max distance that she can climb up the length of the ladder without it slipping? You may assume the ground is perfectly flat, and the wall is perpendicular to the ground.

Answer 1

The max distance is
`z= 2.588 m`

Step-by-step explanation:

A sketch of this question is shown on the first uploaded image

From the question we are told that

The length of the ladder is
`L = 3m`

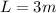
The angle with respect to the horizontal is
`\theta = 50^o`

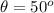
The coefficient of static friction is
`\mu = 0.55`

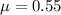
The mass of sally is
`m_s = 60kg`

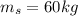
The mass of ladder is
`m_l = 80kg`

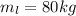
The frictional force acting between the ladder and the ground is mathematically represented as

`F_F = \mu (m_sg + m_l g)`

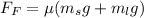
Where g is the acceleration due to gravity

Substituting values

`F_F = 0.55(60*9.8 + 80*9.8 )`

`= 754.6N`

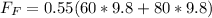
For the ladder not to slipping the frictional force must be equal to the Normal force

Which implies that the normal force
`F_N`
`= 754.6N`

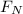
Let assume that sally is at a distance z from point B as shown in the diagram

Form the ladder to slip then the net torque about must be equal to zero

The net torque is mathematically represented as

`F_N L sin \theta - m_lg*(L)/(2) cos \theta - m_s g z cos \theta = 0`

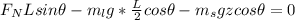
Making z the subject

`z = (F_N L sin \theta - m_l * g * (L)/(2) cos \theta )/(m_s g cos \theta)`

`= (754.6 *3 sin 50 - 80 * 9.8 *1.5\ cos 50 )/(60 * \ 9.8 \ cos 50)`

`z= 2.588 m`