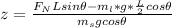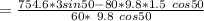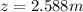Answer:
The max distance is
Step-by-step explanation:
A sketch of this question is shown on the first uploaded image
From the question we are told that
The length of the ladder is
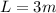
The angle with respect to the horizontal is
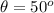
The coefficient of static friction is
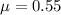
The mass of sally is
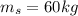
The mass of ladder is
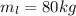
The frictional force acting between the ladder and the ground is mathematically represented as
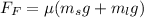
Where g is the acceleration due to gravity
Substituting values
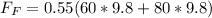
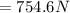
For the ladder not to slipping the frictional force must be equal to the Normal force
Which implies that the normal force
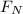
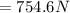
Let assume that sally is at a distance z from point B as shown in the diagram
Form the ladder to slip then the net torque about must be equal to zero
The net torque is mathematically represented as
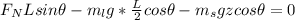
Making z the subject