Question

Find the value of x to the nearest hundredth. Assume that segments that appear to be tangent are tangent.

Answer 1

x = 9

Explanation:

Tangent at S = R = Q

3x - 8 = x + 10

2x = 18

x = 9

Answer 2

Given:

Given that A and B are circles.

The lines TQ and TS are tangent to the circles A and B.

The length of the tangent TQ is (3x - 8)

The length of the tangent TS is (x + 10)

We need to determine the value of x.

Value of x:

Since, the tangents TQ and TS meet at the common point T, then by two tangents theorem, we have;

`TQ = TS`

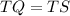
Substituting the values, we have;

`3x-8=x+10`

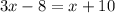
Simplifying, we get;

`2x-8=10`

`2x=18`

`x=9`

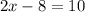
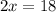
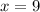
Thus, the value of x is 9.