Answer:
(2, 2)
Explanation:
First find the slope of the line MN, using the two given points:
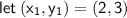
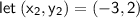
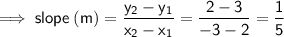
If two lines are perpendicular to each other, the product of their slopes will be -1.
Therefore, the slope (m) of the line perpendicular to MN is:
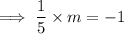
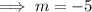
Using the point-slope form of the linear equation with point K (3, -3), we can construct the linear equation of the line perpendicular to MN:
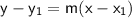
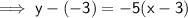
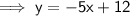
Now we have the equation of the line perpendicular to MN, we can input the x-values of the solution options to see which once is correct:
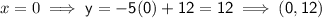
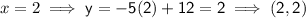
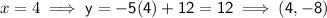
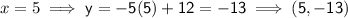
Therefore, the point that is on the line that is perpendicular to MN and passes through point K is (2, 2)