Question

On a coordinate plane, line M N goes through points (2, 3) and (negative 3, 2). Point K is at (3, negative 3). Which point could be on the line that is perpendicular to Line M N and passes through point K? (0, −12) (2, 2) (4, 8) (5, 13)

Answer 1

MN goes through

• (2,3)
• (-3,2)

Slope:-

• m=2-3/-3-2=-1/-5=1/5

Slope of perpendicular line:-

• -5

Passes through k(3,-3)

Equation in point slope form

• y-y1=m(x-x1)
• y+3=-5(x-3)
• y+3=-5x+15
• y=-5x+12

Check one by one

• 0=-5(-12)+12=60+12=72
• 2=-5(2)+12=-10+12=2

Yes option B is correct

Answer 2

(2, 2)

Explanation:

First find the slope of the line MN, using the two given points:

`\sf let\:(x_1,y_1)=(2,3)`

`\sf let\:(x_2,y_2)=(-3,2)`

`\implies \sf slope\:(m)=(y_2-y_1)/(x_2-x_1)=(2-3)/(-3-2)=\frac15`

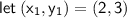
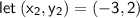
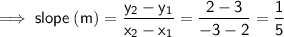
If two lines are perpendicular to each other, the product of their slopes will be -1.

Therefore, the slope (m) of the line perpendicular to MN is:

`\implies \frac15 * m=-1`

`\implies m=-5`

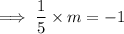
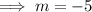
Using the point-slope form of the linear equation with point K (3, -3), we can construct the linear equation of the line perpendicular to MN:

`\sf y-y_1=m(x-x_1)`

`\implies \sf y-(-3)=-5(x-3)`

`\implies \sf y=-5x+12`

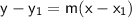
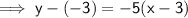
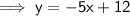
Now we have the equation of the line perpendicular to MN, we can input the x-values of the solution options to see which once is correct:

`x=0\implies \sf y=-5(0)+12=12\implies (0,12)`

`x=2\implies \sf y=-5(2)+12=2\implies (2,2)`

`x=4\implies \sf y=-5(4)+12=12\implies (4,-8)`

`x=5\implies \sf y=-5(5)+12=-13\implies (5,-13)`

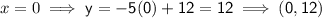
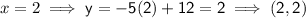
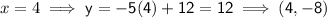
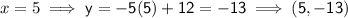
Therefore, the point that is on the line that is perpendicular to MN and passes through point K is (2, 2)