Answer:
The interquartile range (IQR) of the data set is 3.
Explanation:
Given : Data set 2.6, 3, 4.9, 5, 5, 6, 6, 7.9, 8, 8.2.
To find : The interquartile range (IQR) of the data set ?
Solution :
Arrange the terms in ascending order.
2.6 , 3 , 4.9 , 5 , 5 , 6 , 6 , 7.9 , 8 , 8.2
Find the median of the data,
The median is the middle term in the arranged data set. In the case of an even number of terms, the median is the average of the two middle terms.
i.e.
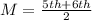 term
term
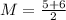
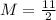
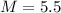
The lower half of data is the set below the median.
i.e. 2.6 , 3 , 4.9 , 5 , 5
The middle term is median.
First quartile=4.9
The upper half of data is the set below the median.
i.e. 6 , 6 , 7.9 , 8 , 8.2
The middle term is median.
Third quartile=7.9
The interquartile range is the difference between the first quartile and the third quartile,
i.e.
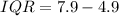
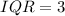
Therefore, the interquartile range (IQR) of the data set is 3.