Question

Assume we choose an American household at random and let the random variable X be the number of cars (including SUVs and light trucks) they own. Here is the probability model if we ignore the few households that own more than five cars. Cars (X) 0 1 2 3 4 5 P(X) 0.09 0.36 0.35 0.13 0.05 0.02 Suppose the cost of gas plummets and the price of cars drastically drops, so that every household purchases an additional 3 cars, so that now the values of X are 3, 4, 5, 6, 7, 8 with the corresponding probabilities remaining the same. What happens to the mean (expected) number of cars owned?

Answer 1

The mean would increase by 3

Explanation:

The number cars and their probability is shown on the first uploaded image

The mean for the number of cars[X] owned can be mathematically represented as

`E(x) = \sum [ x P(x= x)]`

From the question we are told that each household purchased additional three cars

Let Z be the random variable for the number of cars when the the additional car where added

So Mathematically

Z = X + 3

The mean for the number of cars[X + 3] owned can be mathematically represented as

`E(Z)= E(X +3) = \sum [ (x+3) P(X= x)]`

`= \sum x P(X =x) + 3 \sum P(X =x)`

`= E(x) + 3 \sum (P(X = x))`

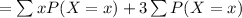
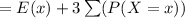
From the above equation we can see that the mean would increase by factor of 3